深入理解HTTPS
Table of Contents
前言 #
感谢伟大的数学家和密码学家们,让我们的网络处于一个相对安全的环境。
最近整理了一下 HTTPS 相关的知识,本文中所有的分析是基于 TLS1.2 版本。
WebTrust #
WebTrust 是由全球两大著名注册会计师协会 AICPA(美国注册会计师协会)和 CICA(加拿大注册会计师协会)共同制定的安全审计标准,主要对互联网服务商的系统及业务运作逻辑安全性、保密性等共计七项内容进行近乎严苛的审查和鉴证。只有通过 WebTrust 国际安全审计认证的根证书才能预装到主流的浏览器中。
CA机构 #
CA机构定义 #
证书颁发机构(CA, Certificate Authority)即颁发数字证书的机构。是负责发放和管理数字证书的权威机构,并作为电子商务交易中受信任的第三方,承担公钥体系中公钥的合法性检验的责任。
有哪些CA机构 #
目前全球主流的 CA 机构有 Comodo 、Symantec、GeoTrust、DigiCert、Thawte、GlobalSign、RapidSSL 等,其中 Symantec、GeoTrust 都是 DigiCert 机构的子公司,目前市场上主流的 SSL 证书品牌是 Comodo 证书、Symantec 证书、GeoTrust 证书、Thawte 证书和 RapidSSL 证书,还有一些不知名的证书机构也是可以颁发数字证书的。
国内的 CA 机构主要有中国金融认证中心(CFCA)、沃通(WoSign)、数安时代(GDCA)和安信证书(AnTruet)等。
对称加密 #
定义 #
采用单钥密码系统的加密方法,同一个密钥可以同时用作信息的加密和解密,这种加密方法称为对称加密,也称为单密钥加密。
常用加密算法 #
DES、AES、RC2、RC4、RC5 等
示例 #
public class DES {
public static String encrypt(String content, String key) {
try {
byte[] encryptionBytes = content.getBytes("UTF-8");
SecureRandom random = new SecureRandom();
DESKeySpec desKey = new DESKeySpec(key.getBytes());
SecretKeyFactory keyFactory = SecretKeyFactory.getInstance("DES");
SecretKey secureKey = keyFactory.generateSecret(desKey);
Cipher cipher = Cipher.getInstance("DES");
cipher.init(Cipher.ENCRYPT_MODE, secureKey, random);
byte[] encryptionBase64Bytes = Base64.getEncoder().encode(cipher.doFinal(encryptionBytes));
return new String(encryptionBase64Bytes);
} catch (Exception e) {
e.printStackTrace();
}
return null;
}
public static String decrypt(String content, String key) {
try {
byte[] decryptionBytes = Base64.getDecoder().decode(content);
SecureRandom random = new SecureRandom();
DESKeySpec desKey = new DESKeySpec(key.getBytes());
SecretKeyFactory keyFactory = SecretKeyFactory.getInstance("DES");
SecretKey secureKey = keyFactory.generateSecret(desKey);
Cipher cipher = Cipher.getInstance("DES");
cipher.init(Cipher.DECRYPT_MODE, secureKey, random);
return new String(cipher.doFinal(decryptionBytes), "UTF-8");
} catch (Exception e) {
e.printStackTrace();
}
return null;
}
public static void main(String[] args) {
final String key = "this_is_key";
String content = "九点下班";
String encryptStr = DES.encrypt(content, key);
System.out.println("加密:" + encryptStr);
String decryptStr = DES.decrypt(encryptStr, key);
System.out.println("解密:" + decryptStr);
}
}
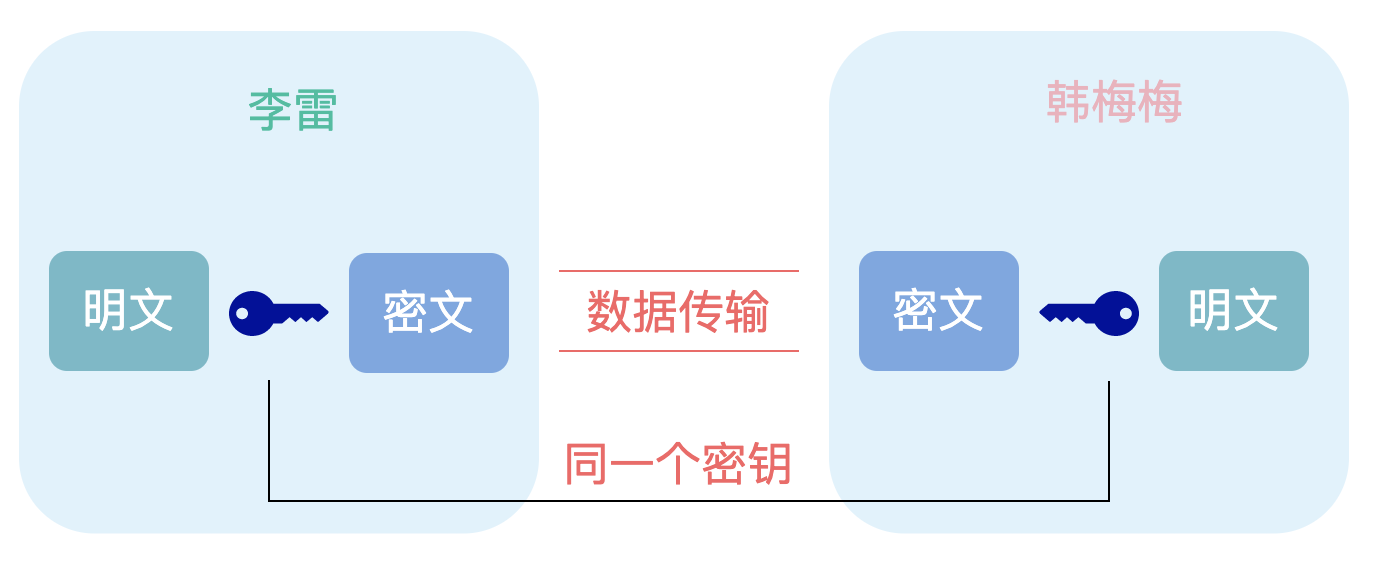
1、李雷想要给韩梅梅发送消息,他们约定使用对称加密的方式把消息进行加密
2、李雷用密钥把消息加密然后发送给韩梅梅
3、韩梅梅用同一个密钥解密,然后看到李雷发送给自己的消息
可以看到使用上面的方式,一旦密钥泄漏,消息就很容易被破解
非对称加密 #
定义 #
对称加密算法在加密和解密时使用的是同一个秘钥,非对称加密算法需要两个密钥来进行加密和解密,这两个密钥是公开密钥(public key,简称公钥)和私有密钥(private key,简称私钥)。
常用加密算法 #
RSA、ECC 等
示例 #
public class RSA {
private static Cipher cipher;
static {
try {
cipher = Cipher.getInstance("RSA");
} catch (NoSuchAlgorithmException e) {
e.printStackTrace();
} catch (NoSuchPaddingException e) {
e.printStackTrace();
}
}
public static void generateKeyPair() {
try {
KeyPairGenerator keyPairGenerator = KeyPairGenerator.getInstance("RSA");
keyPairGenerator.initialize(2048);
KeyPair keyPair = keyPairGenerator.generateKeyPair();
PublicKey publicKey = keyPair.getPublic();
PrivateKey privateKey = keyPair.getPrivate();
String publicKeyStr = getKeyString(publicKey);
String privateKeyStr = getKeyString(privateKey);
System.out.println("publicKeyStr :" + publicKeyStr);
System.out.println("privateKeyStr :" + privateKeyStr);
} catch (Exception e) {
e.printStackTrace();
}
}
public static PublicKey getPublicKey(String key) throws Exception {
byte[] keyBytes = Base64.decode(key);
X509EncodedKeySpec keySpec = new X509EncodedKeySpec(keyBytes);
KeyFactory keyFactory = KeyFactory.getInstance("RSA");
PublicKey publicKey = keyFactory.generatePublic(keySpec);
return publicKey;
}
public static PrivateKey getPrivateKey(String key) throws Exception {
byte[] keyBytes = Base64.decode(key);
PKCS8EncodedKeySpec keySpec = new PKCS8EncodedKeySpec(keyBytes);
KeyFactory keyFactory = KeyFactory.getInstance("RSA");
PrivateKey privateKey = keyFactory.generatePrivate(keySpec);
return privateKey;
}
public static String getKeyString(Key key) {
byte[] keyBytes = key.getEncoded();
return Base64.encode(keyBytes);
}
public static String encrypt(String publicKey, String content) {
try {
cipher.init(Cipher.ENCRYPT_MODE, getPublicKey(publicKey));
byte[] encryptBytes = cipher.doFinal(content.getBytes());
return Base64.encode(encryptBytes);
} catch (Exception e) {
e.printStackTrace();
}
return null;
}
public static String decrypt(String privateKey, String content) {
try {
cipher.init(Cipher.DECRYPT_MODE, getPrivateKey(privateKey));
byte[] decryptBytes = cipher.doFinal(Base64.decode(content));
return new String(decryptBytes);
} catch (Exception e) {
e.printStackTrace();
}
return null;
}
public static void main(String[] args) {
// generateKeyPair();
final String publicKey = "使用generateKeyPair生成";
final String privateKey = "使用generateKeyPair生成";
String content = "九点下班";
String encryptStr = encrypt(publicKey, content);
System.out.println("加密:" + encryptStr);
String decryptStr = decrypt(privateKey, encryptStr);
System.out.println("解密:" + decryptStr);
}
}
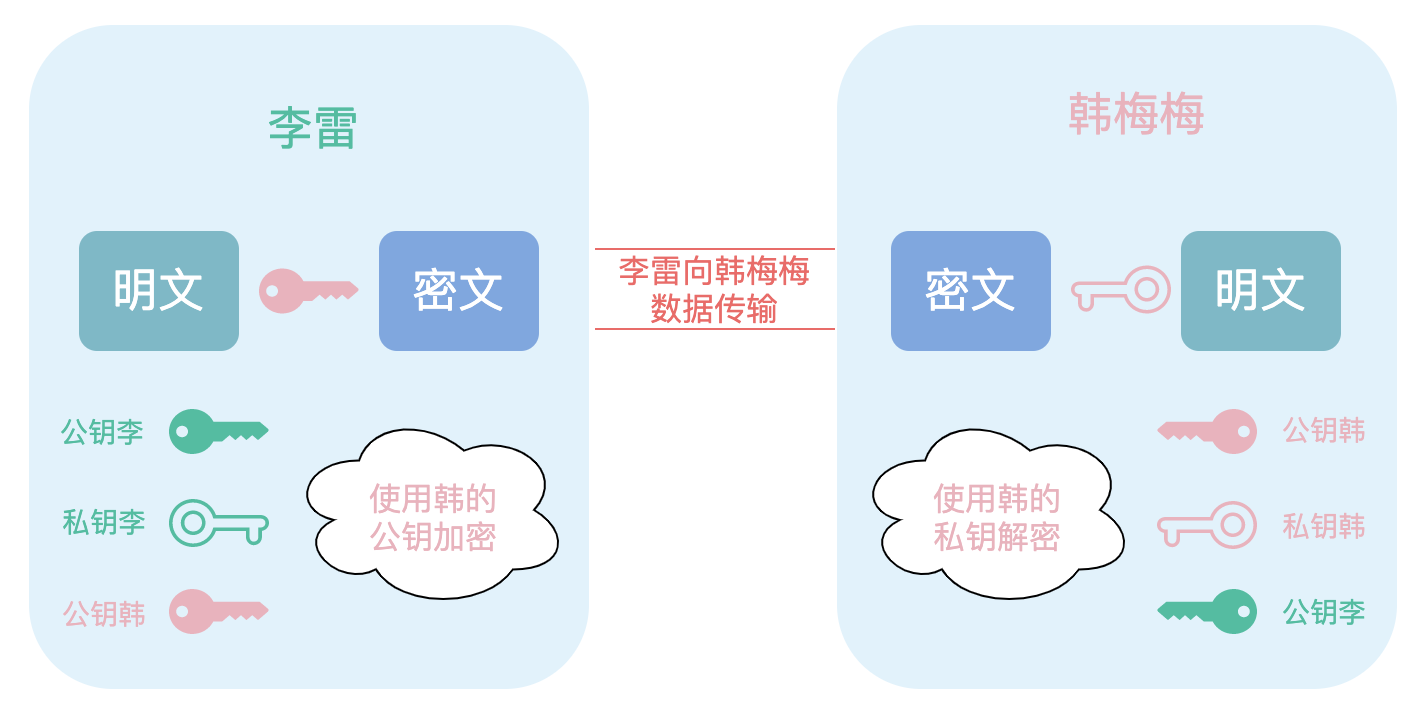
1、李雷想要给韩梅梅发送消息,他们约定使用非对称加密的方式把消息进行加密
2、李雷首先要得到韩梅梅的公钥
2、李雷用韩梅梅的公钥把消息加密然后发送给韩梅梅
3、韩梅梅用自己的私钥解密,然后看到李雷发送给自己的消息
韩梅梅给李雷发送消息同理。
数字签名 #
数字签名(Digital Signature)是一种功能类似写在纸上的普通签名、但是使用了公钥加密领域的技术,以用于鉴别数字信息的方法。一套数字签名通常会定义两种互补的运算,一个用于签名,另一个用于验证。通常我们使用公钥加密,用私钥解密。而在数字签名中,我们使用私钥加密(相当于生成签名),公钥解密(相当于验证签名)。我们可以直接对消息进行签名(即使用私钥加密,此时加密的目的是为了签名,而不是保密),验证者用公钥正确解密消息,如果和原消息一致,则验证签名成功。但通常我们会对消息的散列值签名,因为通常散列值的长度远小于消息原文,使得签名(非对称加密)的效率大大提高。注意,计算消息的散列值不是数字签名的必要步骤。
TLS与SSL #
TLS(传输层安全性协议:Transport Layer Security)及其前身 SSL(安全套接层:Secure Sockets Layer)是一种安全协议,目的是为互联网通信提供安全及数据完整性保障。
我们访问我的个人博客 https://oct.cool/,然后用 WireShark 抓包看下 TLS 握手的过程。
WireShark抓包TLS握手 #
TLS 握手有 RSA 握手、ECDH 握手。通过我下面的抓包分析,下面的示例中使用的是 ECDH 握手。使用 WireShark 进行 ip 过滤
ip.dst == 185.199.109.153 or ip.src == 185.199.109.153
TLS 握手过程如下图,我们现在只关注 Protocol 为 TLSv1.2 的抓包信息:
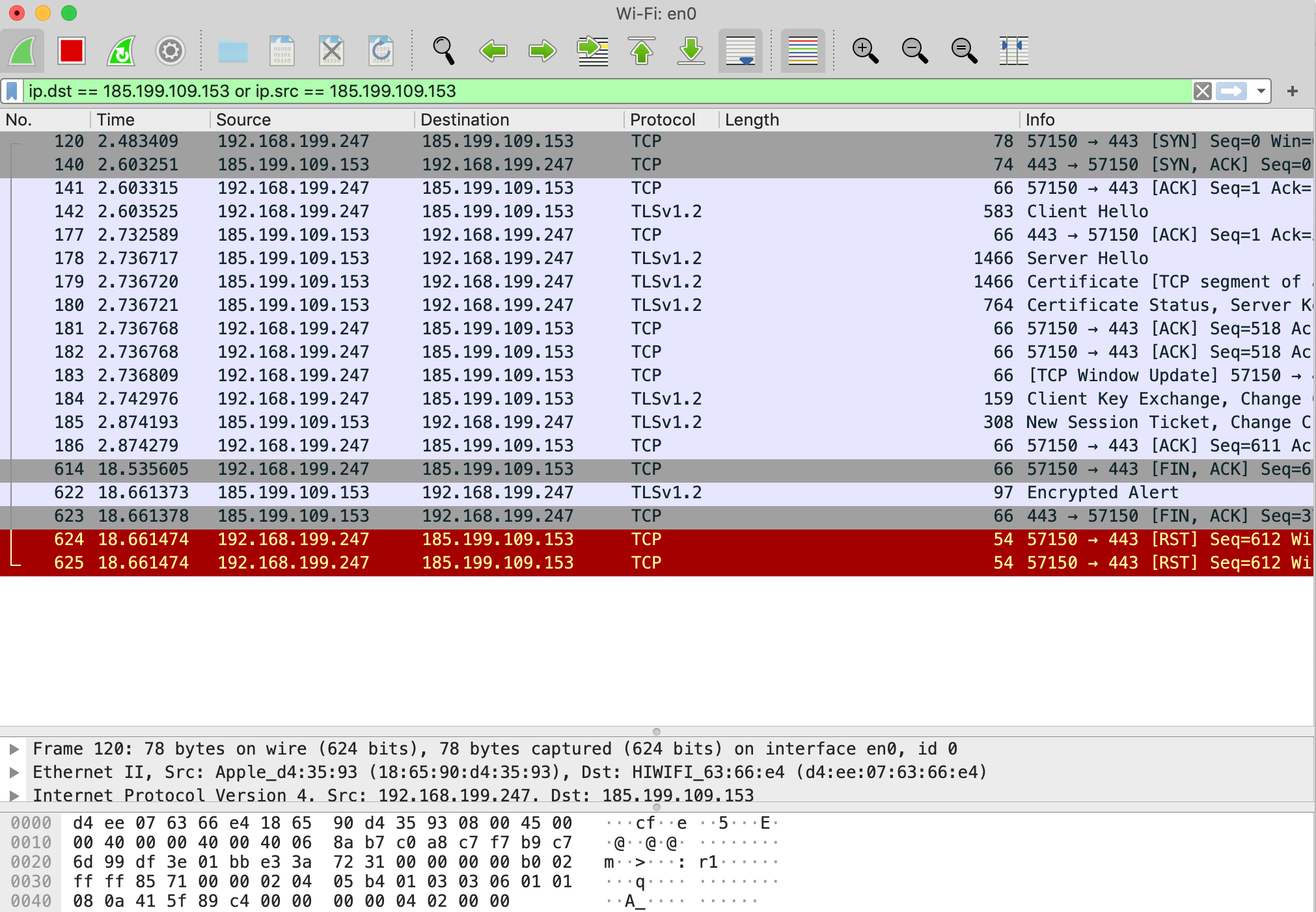
通过上面的图我们可以发现,TLS 的握手过程主要分为以下几步。
- Client Hello
- Server Hello
- Certificate
- Server Key Exchange
- Client Key Exchange
其中涉及到了对称加密、非对称加密等算法,我们来对每一步进行分析。
Client Hello #
浏览器发送给服务器
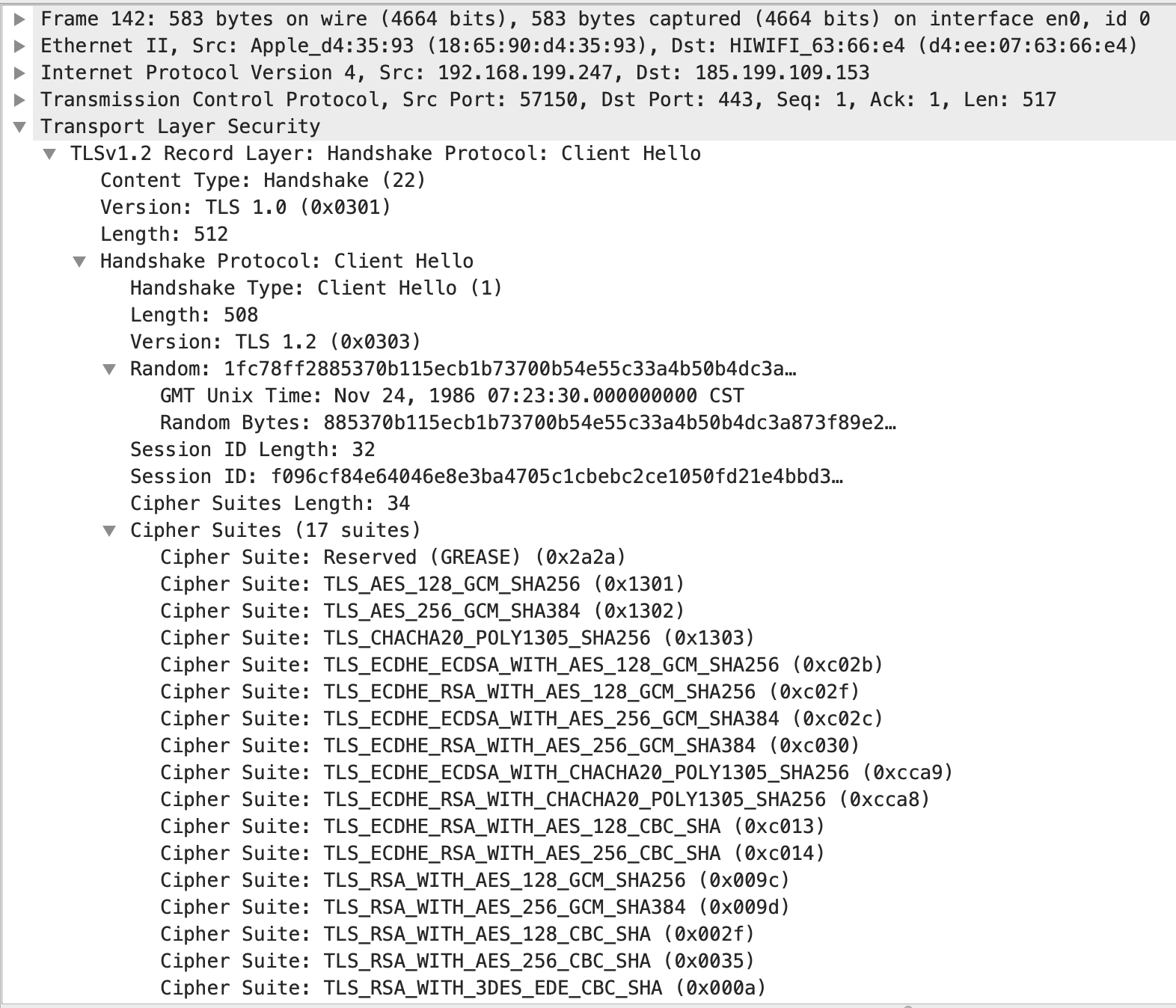
我们需要关注以下内容:
- TLS版本:1.2
- 随机数:Radnom
- 浏览器支持的加密套件:Cipher Suites
可以看到浏览器支持的 Cipher Suites 有17种,服务器会从中选择一个。随机数会在最后计算主密钥(master key)即对称加密所使用的密钥时使用。
Server Hello #
服务器发送给浏览器
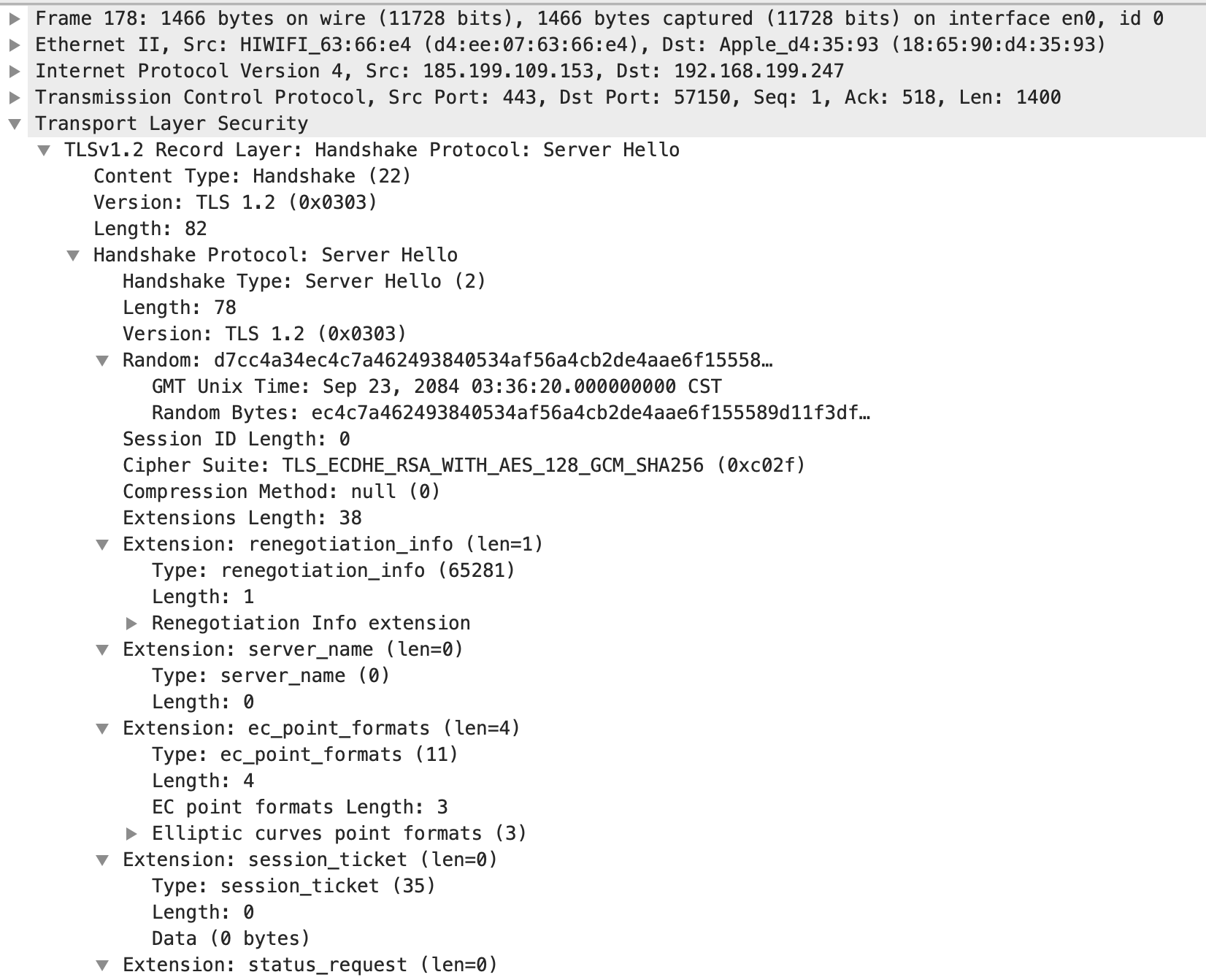
- 随机数:Radnom
- 服务器选择的加密套件:Cipher Suite
可以看到服务器选择的加密套件是:TLS_ECDHE_RSA_WITH_AES_128_GCM_SHA256
我们看下一每一部分的含义
ECDHE:密钥协商算法
RSA:证书公钥加密算法
AES_128:对称加密算法、AES的密码长度
GCM:AES加密模式
SHA256:验证消息的消息摘要算法(哈希算法)
Certificate #
服务器发送给浏览器
在 Server Hello 过程中服务器已经选择好了加密套件。服务器下发证书,携带了 CA 证书链和证书的公钥。在证书链最上层有一个根 CA 证书,这个证书存储在浏览器或者操作系统中,由系统直接信任的。
我们先在浏览器中看一下证书链如下:
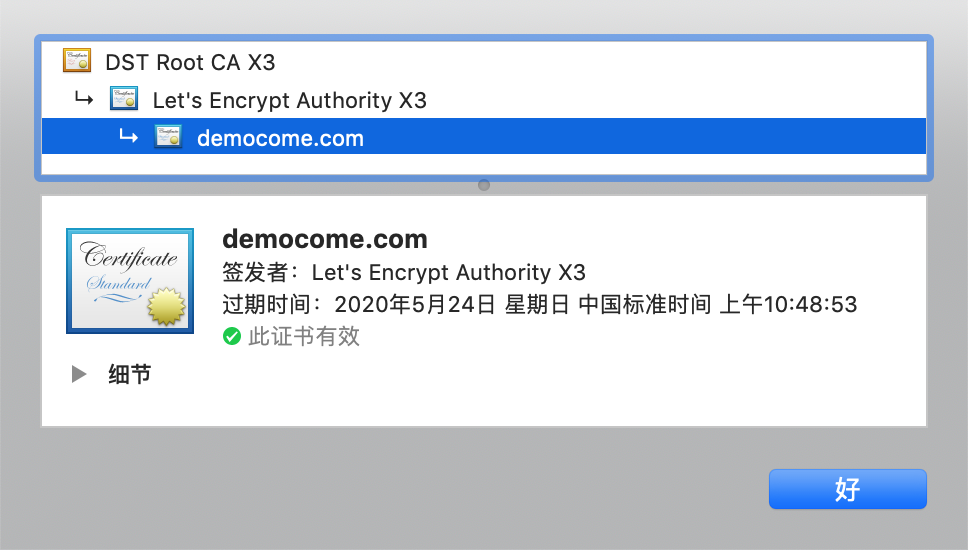
然后再看一下 macOS 系统根证书,可以发现最上层的证书是系统信任的。

浏览器验证服务器证书的过程如下,首先找到找到 democome.com 证书的中级证书颁发机构 Let’s Encrypt Authority X3 ,然后再往上找直到根证书,这里就是 DST Root CA X3。
然后从根证书开始往下去验证数字签名。在这个例子中用 DST Root CA X3 的公钥验证 Let’s Encrypt Authority X3 证书的数字签名。再用 Let’s Encrypt Authority X3 证书的公钥验证服务器证书 democome.com 的数字签名。如果在验证过程中任何一个环节失败,那么这个证书就是不合法的。
Certificate 这一步骤信息如下
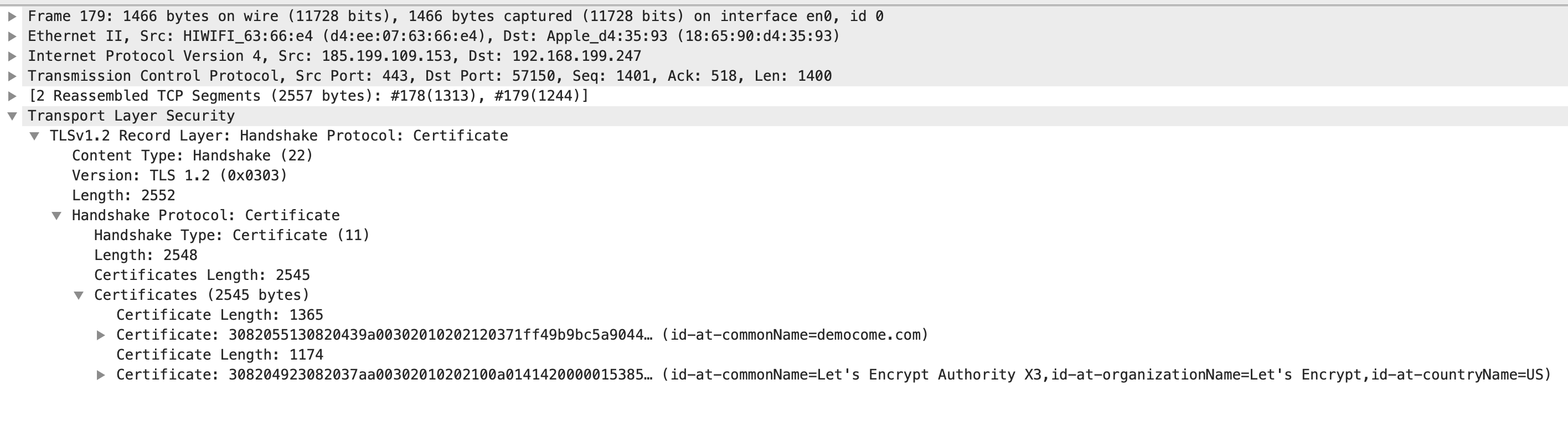
证书的公钥如下图:
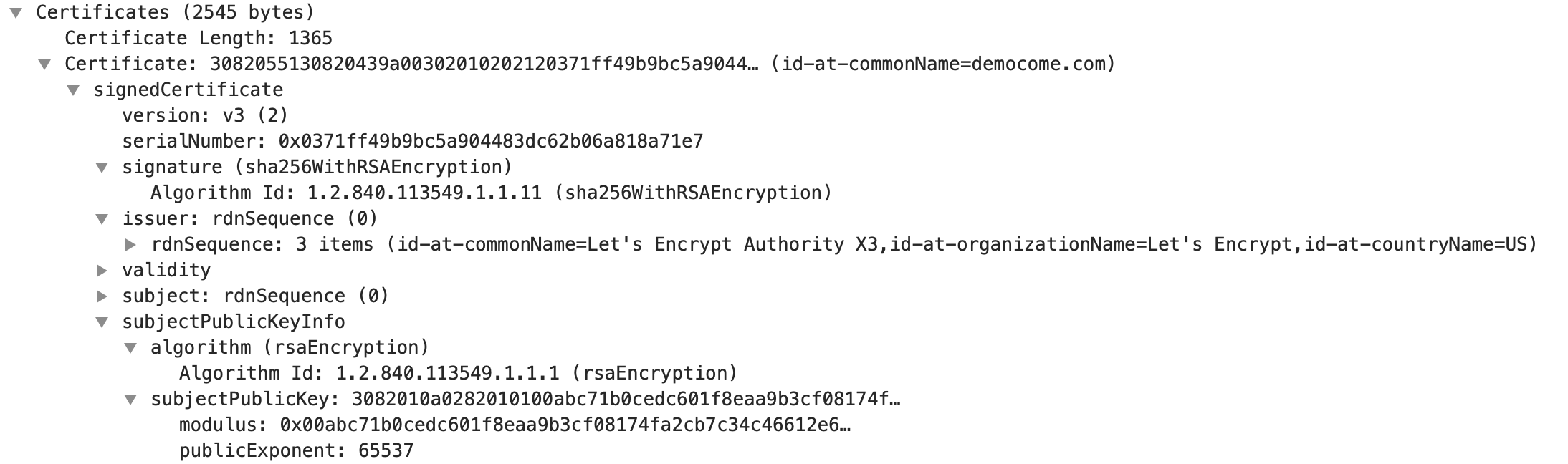
证书签名如下图:
证书的签名用来确保证书没有被篡改过。

Server Key Exchange #
服务器发送给浏览器
服务器选择的加密套件为:TLS_ECDHE_RSA_WITH_AES_128_GCM_SHA256 其中 ECDHE(Elliptic Curve Diffie Hellman Ephemeral)用于密钥协商。这里涉及到了椭圆曲线加密。椭圆曲线密码(Elliptic Curve Cryptography,缩写:ECC)是一种基于椭圆曲线数学的公开密钥加密算法。ECC 的主要优势是在某些情况下它比其他的算法(比如 RSA 加密算法)使用更小的密钥并提供相当的或更高等级的安全。
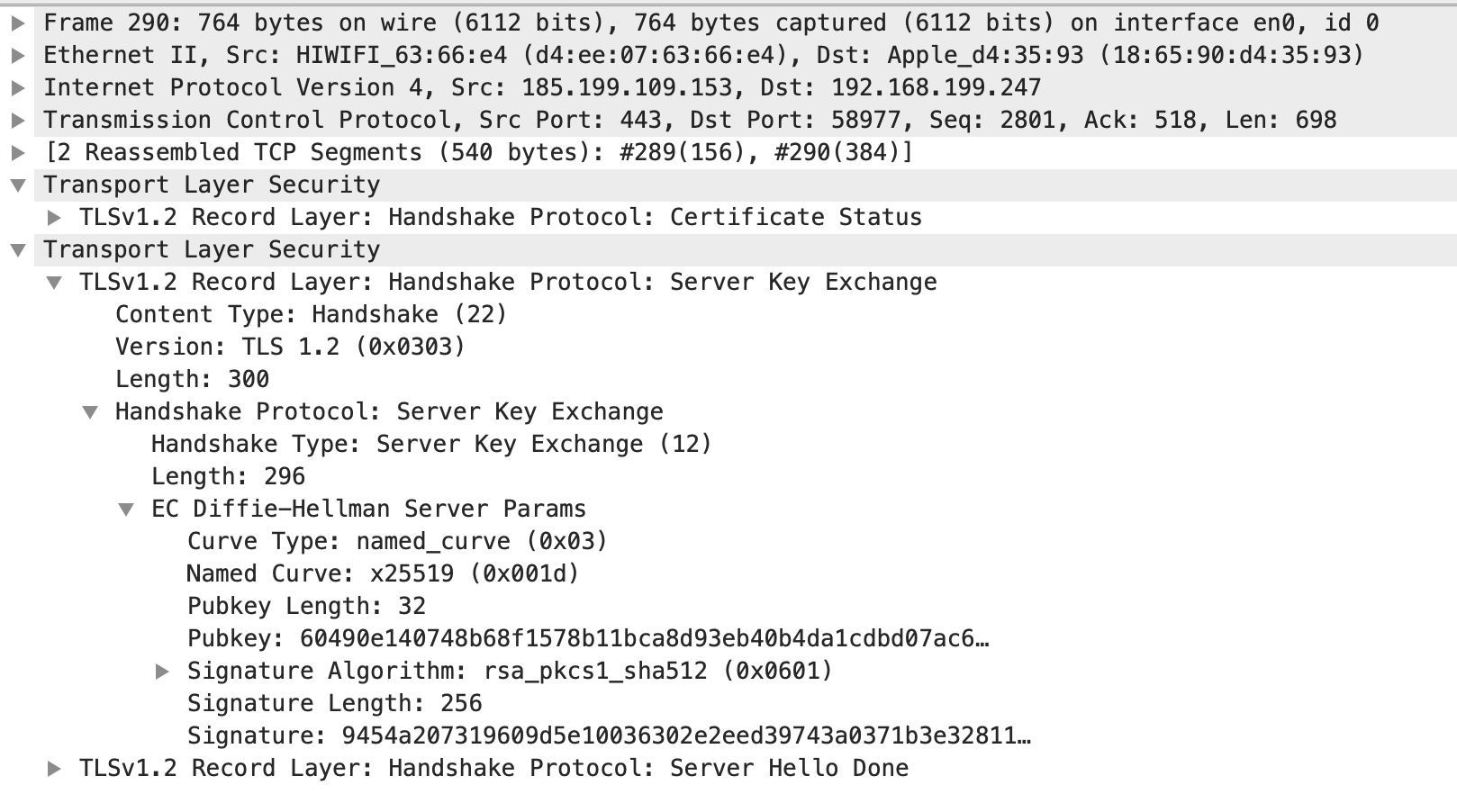
以上 Server Key Exchange 内容我们重点关注 EC Diffie-Hellman Server Params,可以看到 Named Curve 这里选择的是 x25519 这条曲线。它的原理可以简单理解如下:
还是李雷和韩梅梅要写信
1、李雷用自己的私钥 $a$ 算出椭圆曲线上点 $Q1$,然后把基点 $G$ 和 $Q1$ 发送给韩梅梅
2、韩梅梅用自己的私钥 $b$ 算出椭圆曲线上点 $Q2$ 发送给李雷
3、根据椭圆曲线计算规则双方共同计算出的 $K$ 是相同的。
这样就可以进行对称加密了,并且加密的密钥没有在网络上传递过。其实这个计算出来的 $K$ 也不是最终对称加密的密钥这里可以理解为 premaster key ,最终还会用浏览器和服务器双方的随机数再进行一个计算(PRF)得到真正的对称加密密钥 master key。
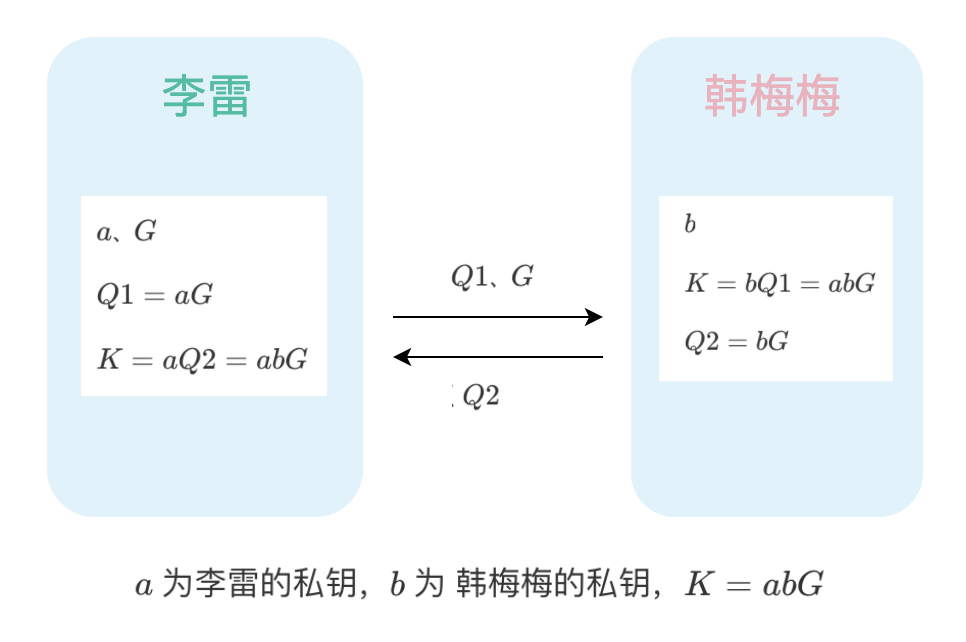
上图中的 Pubkey 就可以理解为服务器计算的椭圆上一点。
以下内容主要是椭圆曲线加密算法的一些数学原理,不感兴趣可以忽略,直接到 Client Key Exchange 这一步骤。
DH 算法 #
DH(Diffie–Hellman key exchange)它可以让双方在完全没有对方任何预先信息的条件下通过不安全信道创建起一个密钥。这个密钥可以在后续的通讯中作为对称密钥来加密通讯内容。
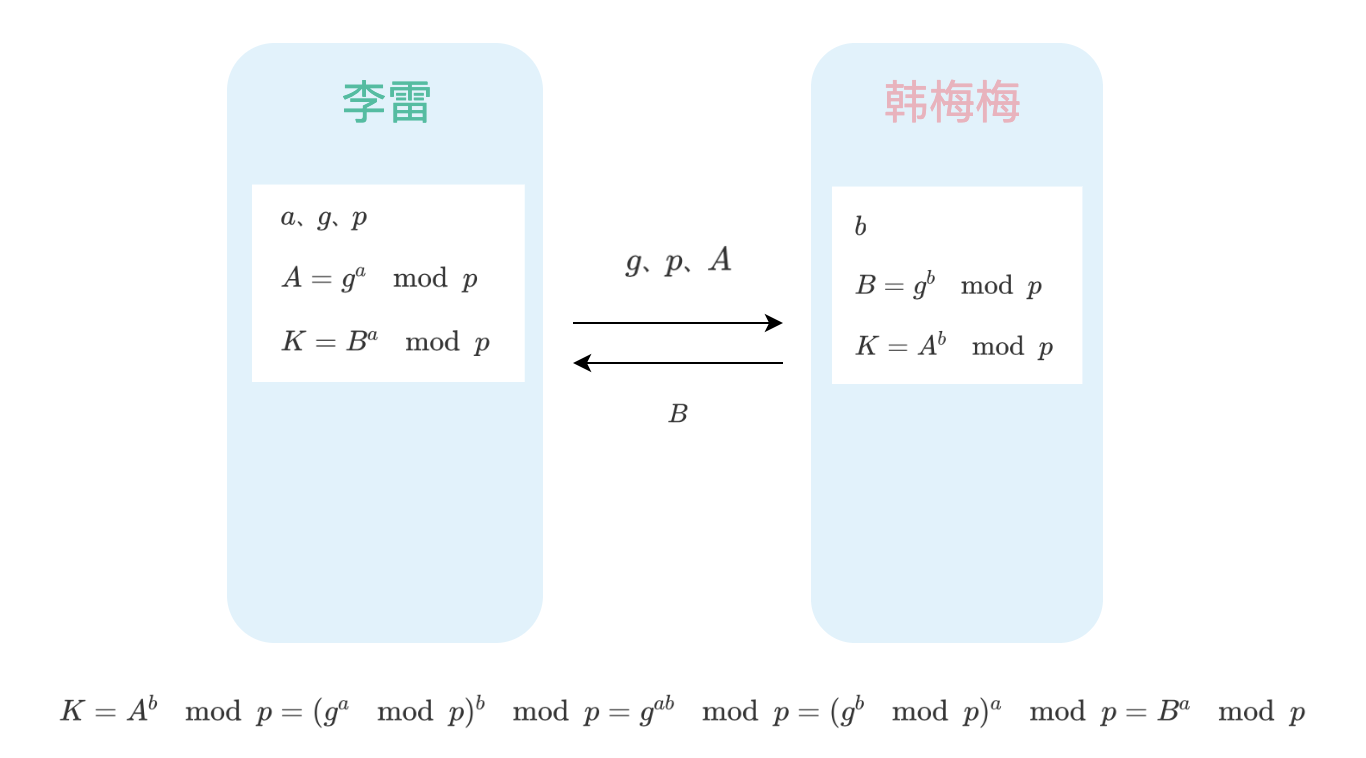
简单解释一下,假如通信的双方是 李雷 和 韩梅梅
前提条件:
- $a$ 是 李雷 的私钥,$b$ 是 韩梅梅 的私钥。
- $p$ 是一个质数,是公开的
- $g$ 是 $p$ 的一个原根,是公开的
协商过程:
第一步:李雷 根据自己的私钥 $a$ 计算出自己的 公钥 $A = g^a\mod p$
第二步:李雷 将 $g$、$p$ 和 $A$ 发送给 韩梅梅
第三步:韩梅梅 根据自己的私钥 $b$ 计算出自己的 公钥 $B = g^b\mod p$
第四步:韩梅梅 把自己的公钥 $B$ 发送给 李雷
第五步:李雷 计算对称加密的密钥 $K=B^a\mod p$
第六步:韩梅梅 计算对称加密的密钥 $K=A^b\mod p$
由上图的推导可知最终计算的 $K$ 是相同的。
具体例子:
李雷 与 韩梅梅 协定使用 $p=23$以及$g=5$。 李雷 的私钥 $a=6$, 计算$A = g^a\mod p$并发送给 韩梅梅。 $A = 5^6\mod 23 =8$ 韩梅梅 的私钥 $b=15$, 计算$B = g^b\mod p$ 并发送给 李雷。 $B = 5^{15}\mod 23 = 19$ 李雷 计算 $K=B^a\mod p$ $K=19^6\mod 23 = 2$ 韩梅梅 计算 $K=A^b\mod p$ $K=8^{15}\mod 23 = 2$
可以看到对称加密的密钥 $K$ 并没有在 李雷 和 韩梅梅 之间传输,但是计算出来的结果是一样的。
ECC算法 #
椭圆曲线密码(Elliptic Curve Cryptography,缩写:ECC)是一种基于椭圆曲线数学的公开密钥加密算法。ECC的主要优势是在某些情况下它比其他的算法(比如RSA加密算法)使用更小的密钥并提供相当的或更高等级的安全。
椭圆曲线的方程如下:
$y^2 = x^3 + ax + b$
椭圆曲线的函数图像如下:
$y^2 = x^3 - x + 1$
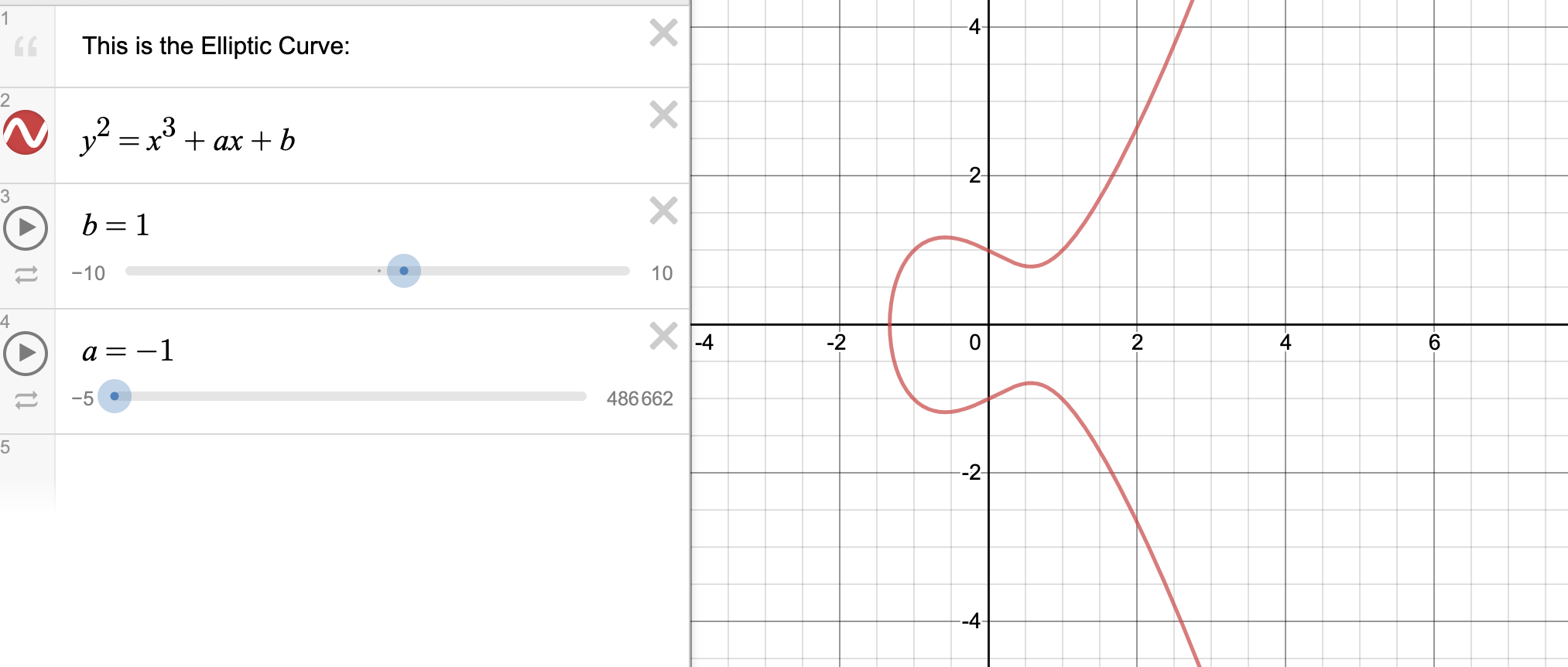
$y^2 = x^3 + x + 1$
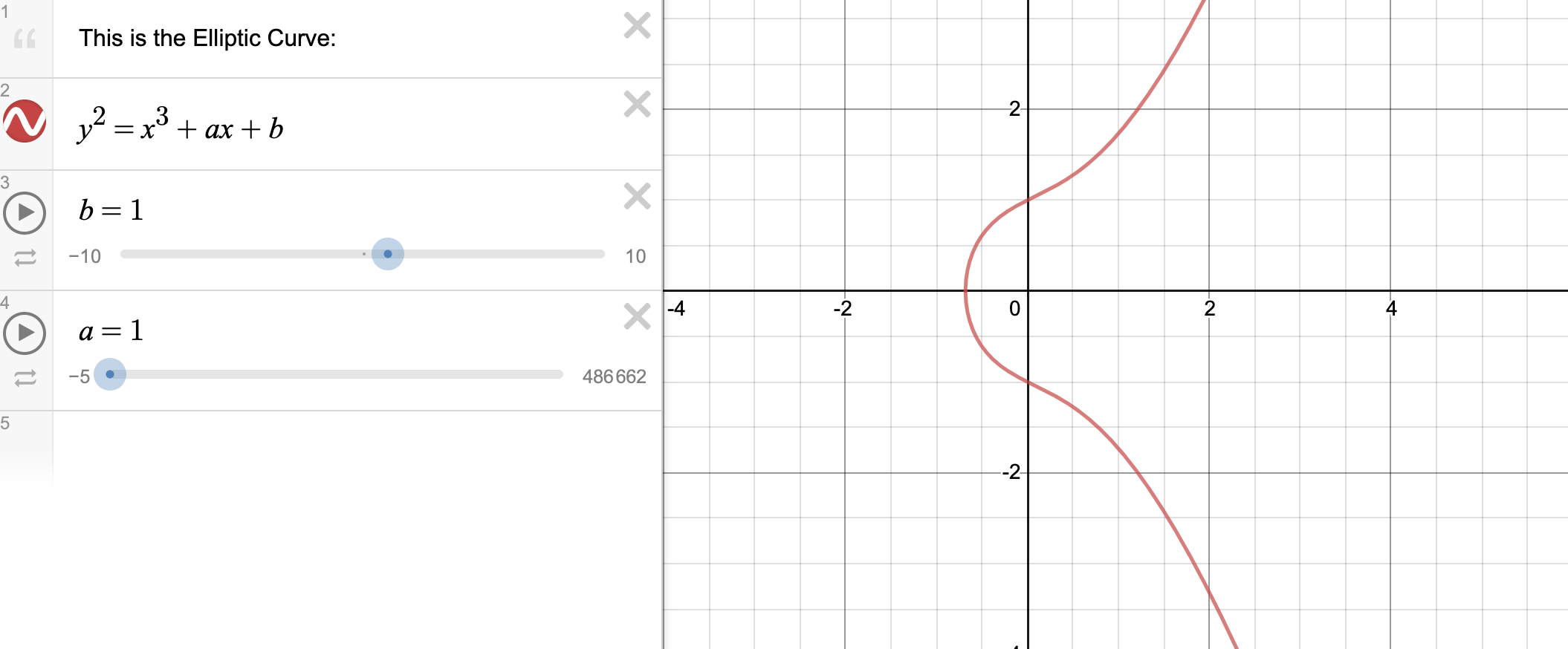
可以看到是关于 X 轴对称的。
椭圆曲线运算 #
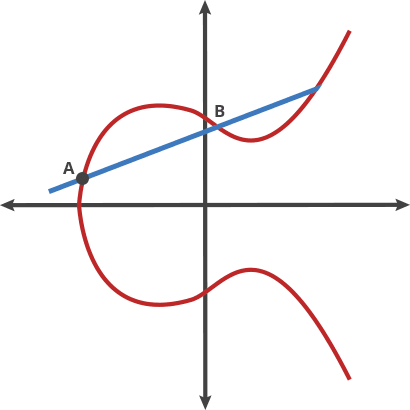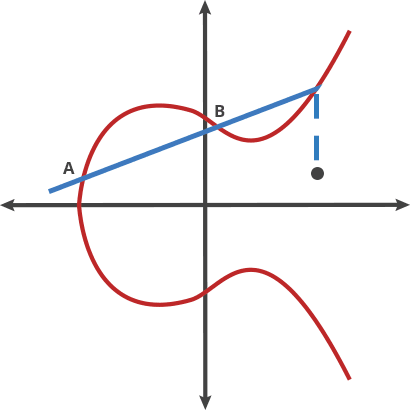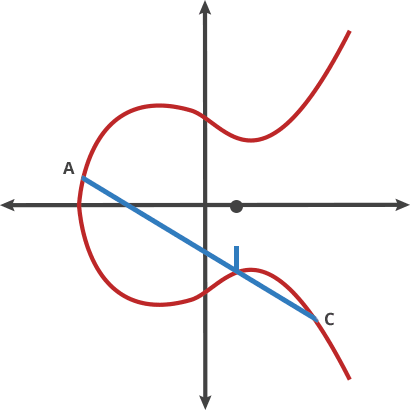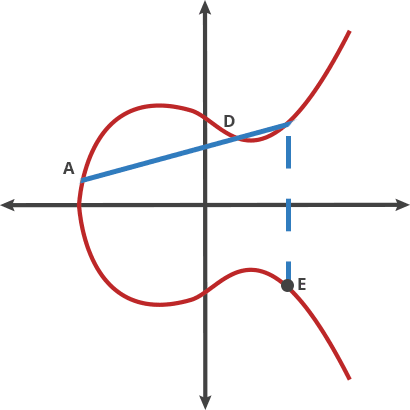
过曲线上 A、B 两点与椭圆曲线交与点 C,点 C 关于 A 轴做对称,与椭圆曲线的交点定义为 A+B。
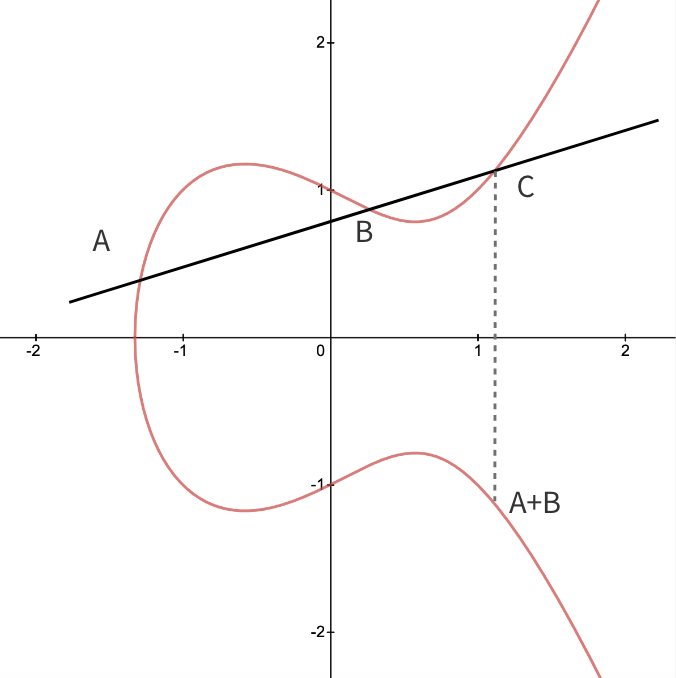
考虑加法的一种特殊情况,如果 A = B,也就A(B)是椭圆曲线的切点,这个时候在重复上面的运算得到 A+A = 2A。
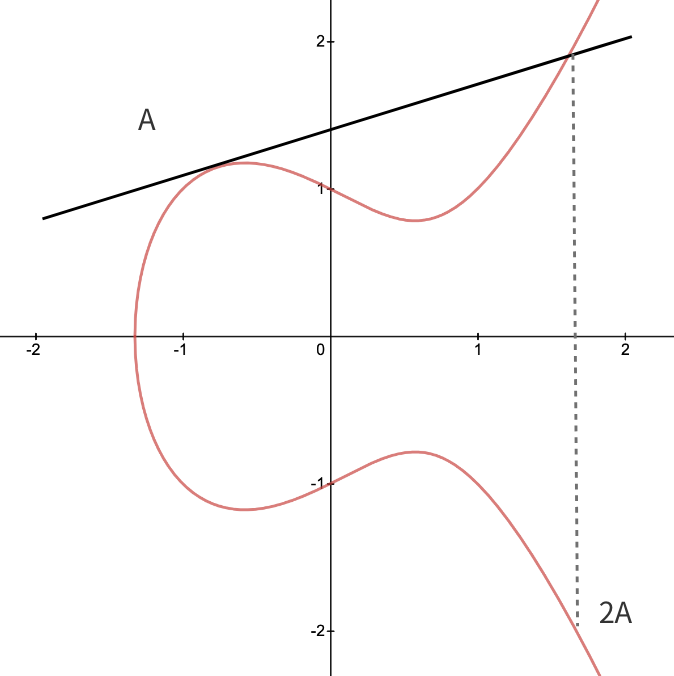
A 关于 X 轴做对称得到的点定义为 -A。
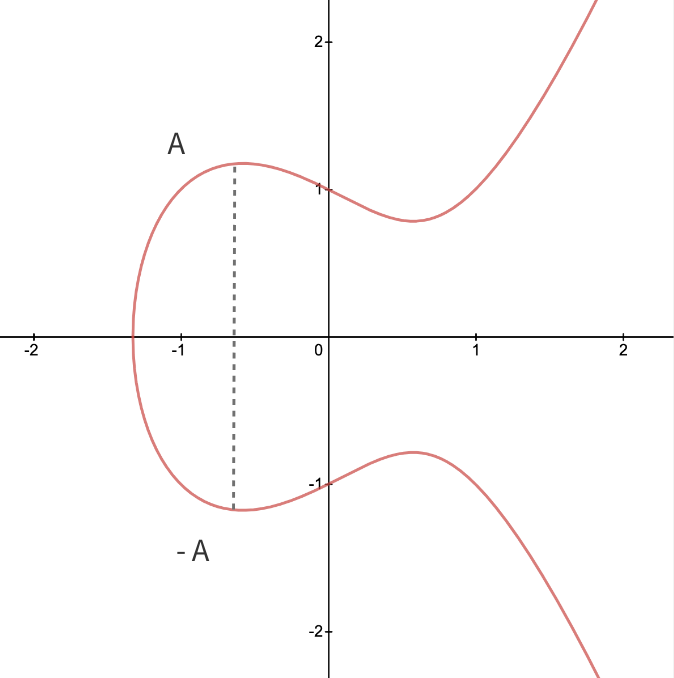
下面有两张动态图,描述了这一过程:
A+B = C
A+C = D
A+D = E
A 和 B 重合演示如下:
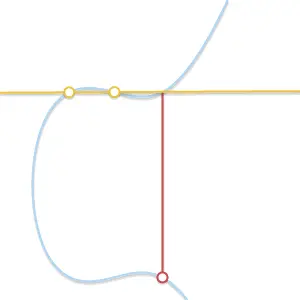
有了以上 $A+B$ 和 $2A$ 的运算,如果已知椭圆曲线上一点 $G$ ,我们可以求出 $2G$、 $3G=G+2G $ 、$4G=2G+2G$ 、$5G=2G+3G$ 、… $kG$,但是反过来如果我们已知 $kG$ ,要想求出 $G$ 是非常困难的。
椭圆曲线的有限域
椭圆曲线加密算法并非使用实数域,而是使用有限域,那么我们把椭圆曲线定义在有限域上。
用 $Ep(a,b)$ 表示椭圆曲线方程 $y^2=x^3+ax+b$ ,在有限域 $Fp$ 中,表示所有在同余( $mod$ )意义上满足该方程的 $(x, y)$ 点。
举例:加入我们的曲线是 $E_{23}(1, 1)$ 即 $p=23,a=1,b=1$ 。那么 $y^2=x^3+x+1$。
点 $P(3, 10)$ 满足 $y^2=10^2=100 ,100(mod)23=8$,$x^3+x+1=3^3+3+1=31,31(mod)23=8$
所以点 $P(3, 10)$ 在曲线上。
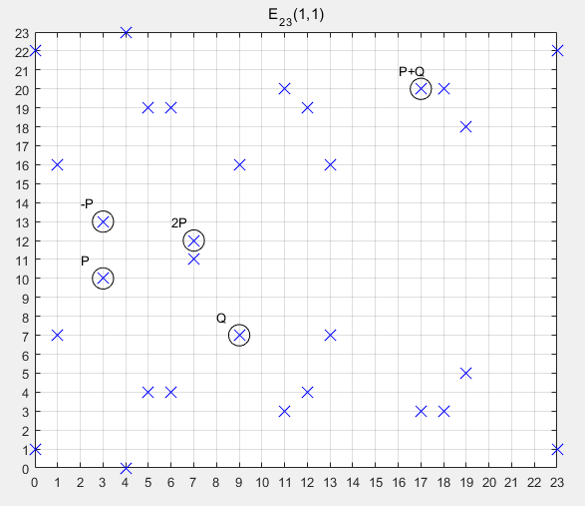
以上是离散化之后的点。利用椭圆曲线进行加密通信的过程如下(这里给出推理过程,涉及到的运算比较复杂,需要的数学知识比较多,我还在研究中):
1、李雷选择一条曲线 $Ep(a,b)$,取椭圆曲线上一点 $G$ 作为基点。
2、李雷选择一个私钥 $k$,然后生成公钥 $K=kG$
3、李雷把 $Ep(a,b)$ 、公钥 $K$ 和 基点 $G$ 传给韩梅梅
4、韩梅梅以上信息,把明文编码到 $Ep(a,b)$ 上一点 $M$,并产生一个随机数 $r$
5、韩梅梅计算 $C_1 = M+rK $ 和 $C_2 = rG$
6、韩梅梅把 $C_1、C_2$ 传给李雷
7、李雷收到信息后,计算 $C_1-kC2$ 结果就是点 $M$
因为 $C_1-kC_2 = M+rK-krG = M+rkG-krG=M$
数学概念 #
有限域 #
在数学中,有限域(finite field)是包含有限个元素的域。与其他域一样,有限域是进行加减乘除运算都有定义并且满足特定规则的集合。有限域最常见的例子是当 $p$ 为素数时,整数对 $p$ 取模。有限域的元素个数称为它的 阶。
群 #
数学里面的群是一类定义了二元运算(我们称之为加法,用符号+表示)的集合。如果想让集合
1、封闭性:如果 $a$ 和 $b$ 属于 $G$,那么 $a+b$ 也属于 $G$;
2、结合律:$(a+b)+c=a+(b+c)$;
3、存在单位元(注:在二元运算中,单位元指与任意元素运算不改变其值的元素,以实数为例,乘法单位元为1,加法单位元为0)$\theta$ 使得 $ a+\theta = \theta + a = a$;
4、每个元素都存在逆元素,也即对于任意元素 $a$ 存在 $b$ 使得 $a+b=\theta$;
如果我们添加第五条要求:
5、交换律:$a+b=b+a$
那么这个群就是阿贝尔群。
Curve25519 #
在密码学中,Curve25519 是一种椭圆曲线,被设计用于椭圆曲线迪菲-赫尔曼(ECDH)密钥交换方法。它是不被任何已知专利覆盖的最快 ECC 曲线之一。
Curve25519 椭圆曲线方程为:$y^2 = x^3 + 486662x^2 + x$,使用基点 $x = 9$
ECDH #
还以 李雷 和 韩梅梅 为例,把 DH 的交换内容改为曲线上的点

当我们选择 Curve25519 是一种椭圆曲线时,参数是确定的,G 也是确定的,所以只交换双方的公钥即可。
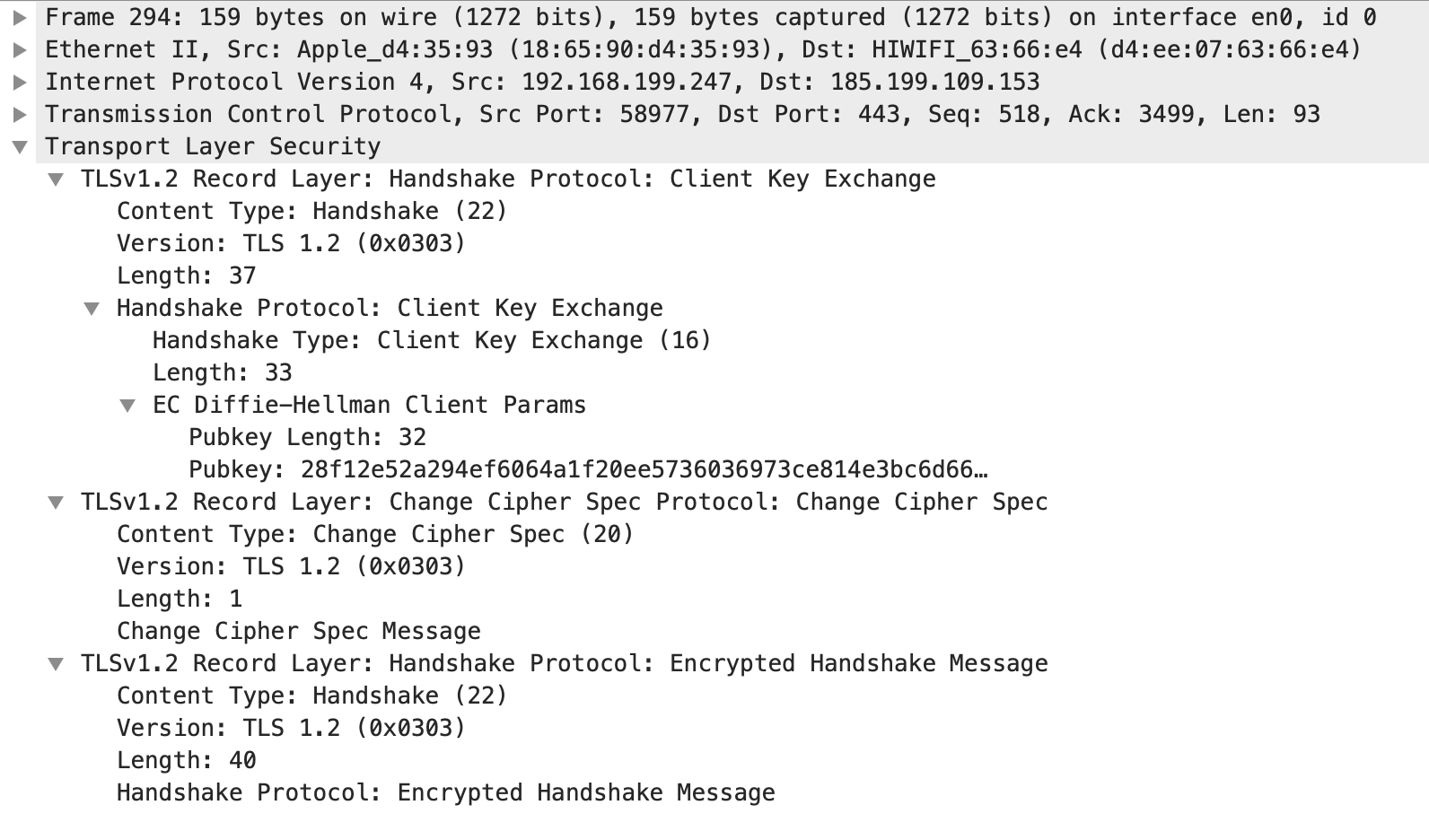
Client Key Exchange #
浏览器发送给服务器
同理,这里的 Pubkey 就可以理解为浏览器计算的椭圆上一点。这一步和 Server Key Exchange 类似,都是为了计算对称加密的密钥。
对称加密通信 #
有了上面的基础,浏览器可以计算出一个对称加密密钥,服务器可以计算出一个对称加密密钥,尽管这两个密钥没有在网络上传输,但是可以保证这两个密钥是相同的。这样使用这个密钥进行加密就可以在网络上进行传输了。
以上就是关于 TLS 握手的基本过程,保证了数据在网络上传递的安全性。
X.509 #
X.509 是密码学里公钥证书的格式标准。X.509 证书已应用在包括 TLS/SSL 在内的众多网络协议里,同时它也用在很多非在线应用场景里,比如电子签名服务。X.509 证书里含有公钥、身份信息(比如网络主机名,组织的名称或个体名称等)和签名信息(可以是证书签发机构 CA 的签名,也可以是自签名)。对于一份经由可信的证书签发机构签名或者可以通过其它方式验证的证书,证书的拥有者就可以用证书及相应的私钥来创建安全的通信,对文档进行数字签名。